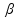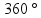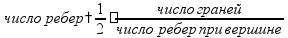|
аксиомы
стереометрии
-
через три точки, не лежащие на одной
прямой, проходит плоскость, и только
одна
-
если две точки прямой лежат в плоскости,
то все точки прямой лежат в этой
плоскости
-
если две плоскости имеют общую точку,
то они имеют общую прямую (пересекаются
по прямой)
|
|
взаимное
расположение прямых
|
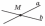
|

|
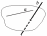
|
|
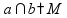
пересекаются
(одна
общая точка)
|
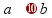
параллельны
(лежат
в одной плоскости и не имеют общих
точек)
|

скрещиваются
(не
лежат в одной плоскости)
|
|
признак
скрещивающихся прямых
|
одна
прямая лежит в некоторой плоскости,
а другая пересекает эту плоскость
в точке, не лежащей на первой прямой
|
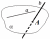
|
|
|
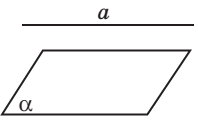
взаимное
расположение прямой и плоскости
|

|
|

|
|
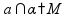
пересекаются
(одна
общая точка)
|
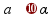
параллельны
(не
имеют общих точек)
|
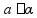
прямая
лежит в плоскости
(все
точки)
|
|
признак
параллельности прямой и плоскости
|
прямая
не лежит в плоскости и параллельна
какой-нибудь прямой, лежащей в этой
плоскости
|

|
|
|
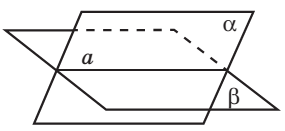
взаимное
расположение плоскостей
|
|

|
|
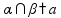
пересекаются
(общая
прямая)
|

параллельны
(не
имеют общих точек)
|
|
признак
параллельности плоскостей
|
две
прямые одной плоскости параллельны
двум пересекающимся прямым второй
плоскости
|
|
|
|
параллельность
в пространстве
|
через
точку пространства, не лежащую на
данной прямой можно провести прямую,
параллельную данной, и только одну
|
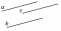
если
две прямые параллельны третьей
прямой, то они параллельны
|

если
одна из параллельных прямых пересекает
плость, то и другая пересекает эту
плоскость
|
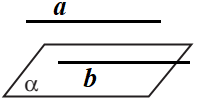
если
одна из параллельных прямых параллельна
плости, то другая либо параллельна
этой плоскости, либо лежит в этой
плоскости
|
|
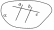
параллельные
прямые, пересекающие данную прямую,
лежат с ней в одной плоскости
|
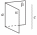
если
прямая параллельна двум пересекающимся
плоскостям, то она параллельна линии
их пересечения
|

если
две плоскости пересечены третьей,
то линии их пересечения параллельны
|
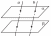
отрезки
параллельных прямых между двумя
параллельными плоскостями равны
|
|
|
угол
между прямыми
|
пересекающимися
|
скрещивающимися
|
|
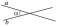
|
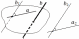
|
|
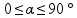
|
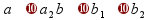
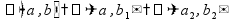
|
|
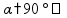
перпендикулярные
прямые
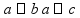
|
|
|
|
перпендикуляр
к плоскости («опущенный»
из точки) -
прямая,
перпендикулярная плоскости (т.е.
любой прямой этой плоскости)
|
|
|
|
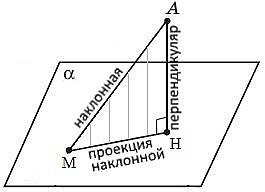
H
- основание перпендикуляра
(проекция
точки на плоскость)
M
- основание наклонной
|
|
угол
между прямой и плоскостью -
угол между прямой и ее проекцией на
эту плоскость
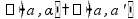
|

|
|
|
двугранный
угол(между
полуплоскостями)равен
углу
между перпендикулярами к ребру
двугранного угла, лежащими на гранях
двугранного угла
|
|

|
угол
между плоскостями
угол
между перпендикуляром к линии
пересечения плоскостей, лежащим в
одной из этих плоскостей, и его
проекцией на другую плоскость
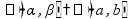
|
|
|
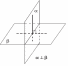
признак
перпендикулярности плоскостей
одна
плоскость проходит через прямую,
перпендикулярную другой плоскости
|
|
|
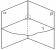
если
плоскость перпендикулярна линии
пересечения двух плоскостей, то она
перпендикуляра этим плоскостям
|
|
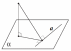
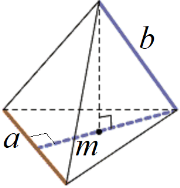
теорема
о трех перпендикулярах
|
|
прямая,
лежащая в плоскости, перпендикулярна
наклонной
 перпендикулярна проекции наклонной
перпендикулярна проекции наклонной
|
|
пр:
|

|
|
|
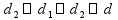
|
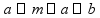
|
|
|
способы
задания плоскости
|
|
расстояния
в пространстве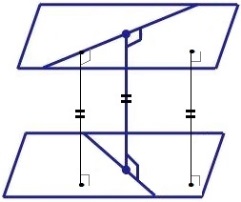
между
точками =
длине
отрезка, соединяющего эти точки
от
точки до прямой =
длине
перпендикуляра, проведенного от точки
до прямой
от
точки до плоскости =
длине
перпендикуляра, опущенного из точки
на плоскость
между
параллельными прямыми
= расстоянию
от любой точки одной прямой до другой
прямой
между
скрещивающимися прямыми
= длине
общего перпендикуляра (илирасстоянию
между параллельными плоскостями,
проходящими через эти прямые, или
расстоянию от любой точки одной прямой
до параллельной ей плоскости, проходящей
через другую прямую)
от
прямой до параллельной ей плоскости
= расстоянию
от любой точки прямой до плоскости
между
параллельными плоскостями=
расстоянию
от любой точки одной плоскости до
другой плоскости
|
|
Многогранники
|
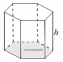
Призма
(плоскости
оснований и боковые ребра параллельны)
площадь
поверхности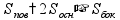
объем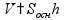
|
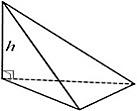
Пирамида
(вершина
и основание - многоугольник)
площадь
поверхности
объем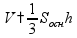
|
|
наклонная
|
прямая
(боковые
ребра
 основанию)
основанию)
|

|
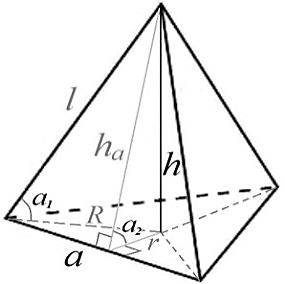
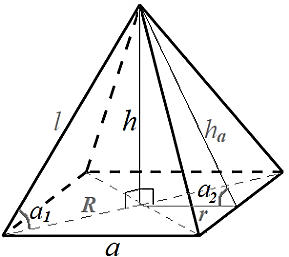
l
- боковое ребро
h
- высота пирамиды
a
- сторона основания
 -
апофема
-
апофема - угол наклона бокового ребра к
основанию
- угол наклона бокового ребра к
основанию
 -
угол наклона боковой грани к основанию
-
угол наклона боковой грани к основанию
r
- радиус вписанной окружности
R
- радиус описанной окружности
|
|
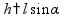
l
- боковое ребро
 -
угол наклона бокового ребра к
основанию
-
угол наклона бокового ребра к
основанию
|
|
h
- высота призмы
|
|
 -
площади основания и боковой поверхности
-
площади основания и боковой поверхности
|
|
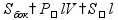
 -
периметр и площадь перпендикулярного
сечения
-
периметр и площадь перпендикулярного
сечения
|
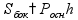
 -
периметр основания
-
периметр основания
|
правильная
(основание
- правильный многоугольник, все
боковые ребра равны)
|
|
|
правильная
(прямая, основание - правильный
многоугольник)
|
треугольная
|
четырехугольная
|
|
|
|
|
параллелепипед
(четырехугольная
призма, основание -параллелограмм)
|
|
наклонный
|
прямой
|
|

состоит
из шести равных по объему пирамид
|
|
|

|
|
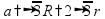
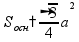
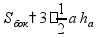
|
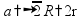
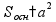
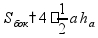
|
|
куб
(все
грани - квадраты)
|
прямоугольный
(прямой,
основание -прямоугольник)
|
|
|
|
в
треугольную пирамиду можно вписать
сферу, причем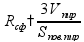
тетраэдр
-
треугольная пирамида
правильный
тетраэдр -
все
ребра равны
|
усеченная
(два
основания)
|
|

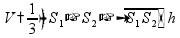
боковые
грани - трапеции
|
|
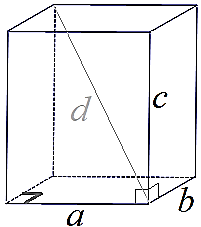
a,
b, c - «измерения» - «линейные размеры»
d
- диагональ параллелепипеда,
диагональное сечение
|
прямоугольная
(боковое
ребро основанию) основанию)
|
|
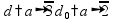

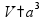
|
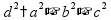
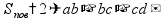
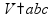
|
|
|
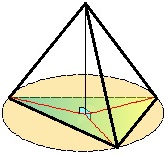
пирамида,
вписанная и описанная окружности
|
-
если все боковые ребра пирамиды
равны, то основание высоты является
центром описанной окружности
|
|
|
-
если
все апофемы пирамиды равны, то
основание высоты является центром
вписанной окружности
|

|
|
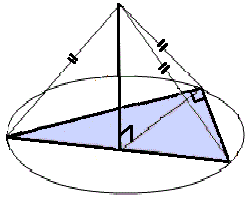
пр:
|
если
в пирамиде все ребра равны, а в
основании - прямоугольный треугольник,
то основание высоты пирамиды лежит
на середине гипотенузы
|
|
площадь
прямоугольной проекции
|
|
свойство
трехгранного угла
|
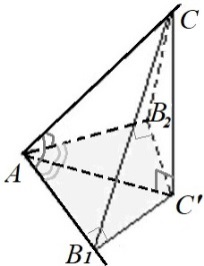
|
если
два плоских угла при вершине
трехгранного угла равны, то их общее
ребро проецируется на биссектрису
третьего плоского угла

|
|
|
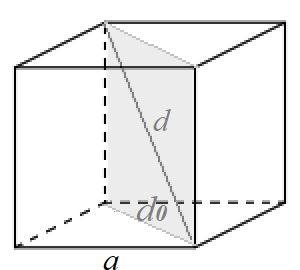
свойство
диагонали куба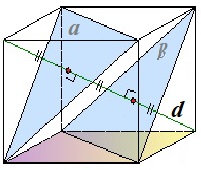
диагональ
 куба куба
 плоскостям
плоскостям
 и и
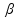
(и
делится на три равных отрезка)
|
|
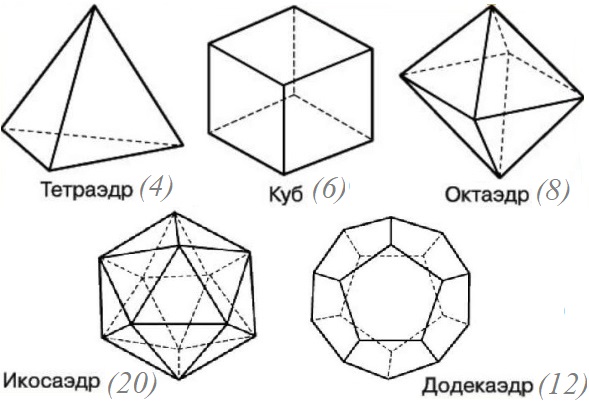
Правильные
многогранники
в
выпуклом многограннике сумма плоских
углов при каждой вершине меньше
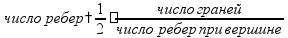
|
|
методы
построения сечений:
|
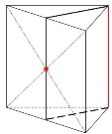
аксиоматический
(построение параллельных прямых)
|
|
|
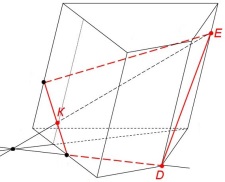
метод
следов (построение проекций прямых
на опорную плоскость)
|
|
|
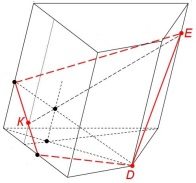
внутреннее
проецирование (построение внутренних
проекций)
|
|
|
|
теорема
Эйлера (для
любого многогранника)
число
вершин + число граней - число ребер = 2
|

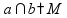
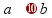

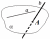



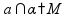
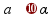
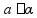


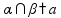


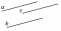

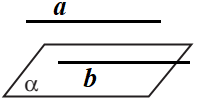


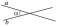
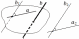
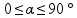
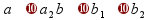
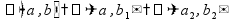
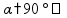
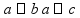



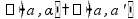


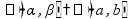



 перпендикулярна проекции наклонной
перпендикулярна проекции наклонной


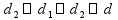
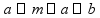







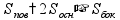
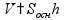

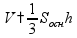

 основанию)
основанию)

 -
апофема
-
апофема - угол наклона бокового ребра к
основанию
- угол наклона бокового ребра к
основанию -
угол наклона боковой грани к основанию
-
угол наклона боковой грани к основанию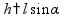
 -
угол наклона бокового ребра к
основанию
-
угол наклона бокового ребра к
основанию -
площади основания и боковой поверхности
-
площади основания и боковой поверхности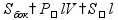
 -
периметр и площадь перпендикулярного
сечения
-
периметр и площадь перпендикулярного
сечения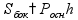
 -
периметр основания
-
периметр основания




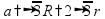
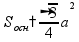
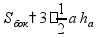
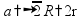
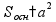
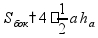


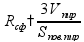

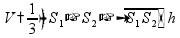
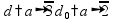

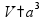
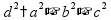
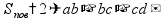
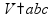








 куба
куба