7 класс. Контрольная работа № 1. I вариант.
- Задайте перечислением элементов множество А={ х| хєZ, |х|<4}
- Найдите значение выражения
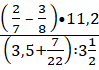
- При каких значениях переменной выражение имеет смысл: а)
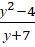; б) 
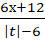
- Найдите значение выражения
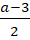для всех целых значений переменной, удовлетворяющих неравенству |a|
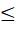3
Варианта |
3 |
4 |
8 |
|
Частота |
2 |
5 |
6 |
3 |
Найдите пропущенную варианту, если среднее арифметическое равно 5.
Найдите объём, размах, моду и медиану ряда.
- Найдите все двузначные числа, зная, что
.
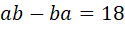Контрольная работа № 1. II вариант.
- Используя характеристическое свойство, запишите множество А натуральных чисел, кратных 11.
- Найдите значение выражения
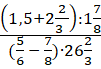. - При каких значениях переменной выражение имеет смысл: а)
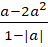б)
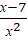
- Найдите значение выражения
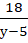для всех целых значений переменной, удовлетворяющих неравенству |у|< 3
Варианта |
6 |
8 |
12 |
|
Частота |
3 |
5 |
6 |
2 |
Найдите пропущенную варианту, если среднее арифметическое равно 8,5. Найдите объём, размах, моду и медиану ряда.
- Найдите все двузначные числа, зная, что
.
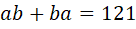Контрольная работа №2
Контрольная работа № 3. Многочлены. Вариант 1
1.Упростите выражение:
а) (3x + 10y) – (6x + 3y) + (6y – 8x); б) p(p2 – 2a) +a(2p – a2);
в) (6х+4)(2 – 3х); г) х2(х – 3)(2+х2)
2. Замените выражение М многочленом так, чтобы получилось тождество: М + (2ху + 3х2) = 2х2 + ху – у2.
3. Упростите выражение - у3 + ху(у – х) – (х2 + у2)(х – у) и найдите его значение при таких значениях переменной, для которых верно равенство |х|=3.
4. Найдите сумму коэффициентов многочлена, тождественно равного выражению (у+3)(у – 5)(у2 +2у – 15) – 225.
5. При каком значении х значение выражения х(2х + 3) – 5(х2 – 3х) + +3х( х – 7) равно 9?
Контрольная работа № 3. Многочлены. Вариант 2.
1.Упростите выражение:
а) (8c2+3c) + ( - 7c2 - 11c + 3) - ( - 3c2 – 4); б) с2(3а – 7с) – с2(5а +3с);
в)(4х – 3)(8х+6); г)2у(у2 – 1)(2+у)
2. Замените выражение М многочленом так, чтобы получилось тождество: М – (х2 + ху + 3у2) = х2 + ху – 2у2
3. Упростите выражение (х3 + 2у)(х2 – 2у) – (х2 + 2у)(х3 – 2у)+4х3у и найдите его значение при таких значениях переменной, для которых верно равенство х=2, а у= | 
.
4. Найдите сумму коэффициентов многочлена. тождественно равного выражению ( - 3n2 + 2n + 1) (3n2 + 2n - 1)+1.
5. При каком значении х значение выражения х(4х +11) – 7(х2 – 5х) + +3х(х + 3) равно 11.
Контрольная работа № 4. Уравнения. I вариант.
1.Решите уравнения: а) 19х – (3х – 4) = 4(5х – 1);
б) 4 (0,25х – 6) = 8(0,125х + 3)
2.Одна из сторон треугольника на 2 см меньше другой и в 2 раза меньше третьей. Найдите стороны треугольника, если его периметр равен 22 см.
3.Найдите множество корней уравнения:
а) (2х + 3)(4х – 3) – 2х(4х + 1) – 17 = 0;
б) 
.
4.В одном элеваторе было зерна в 2 раза больше, чем в другом. Из первого элеватора вывезли 750т зерна, а во второй элеватор привезли 350 т, после чего в обоих элеваторах зерна стало поровну. Сколько тонн зерна было первоначально в каждом элеваторе?
5. При каких значениях m и n уравнение ( m + 3)x = n – 1 не имеет корней?
Контрольная работа № 4. Уравнения. II вариант.
1.Решите уравнения: а) 10x – (2x – 4) = 4(3x – 2);
б)16(0,25х – 1) = 5(0,8х – 3,2).
2. Одна из сторон треугольника на 6 см меньше другой и на 9 см меньше третьей. Найдите стороны треугольника, если его периметр равен 33 см.
3.Найдите множество корней уравнения:
а) (3х – 2)(2х + 3) – 2х(3х +1) – 18 =0;
б) 
.
4.На одном складе 185 т угля, а на другом 237 т. Первый склад отпускал ежедневно по 15 т угля, а второй – по 18 т. Через сколько дней на втором складе угля будет в полтора раза больше, чем на первом?
5.При каких значениях m и n уравнение ( m – 2)х = n + 1 имеет бесконечное множество корней?
Контрольная работа №5. I вариант.
1.Разложите на множители:
а) х2у+ху2; б)а2bc+ab2c+abc2; в)2а+2b+ax+bx; г) х4–3х3+3х2–9х.
2. Решите уравнение: а) 7х2–х = 0 б) 2х3–8х2 +5х–20=0
3. Докажите, что выражение а)88+219 кратно 33; б) 320+318–316 кратно 267
4. Разность двух натуральных чисел равна 1, а их произведение равно 42. Найдите сумму этих чисел.
5. Известно, что при некотором значении переменной а значение выражения а2 +2а– 4 равно 9. Найдите, чему равно при этом же значении а значение выражения:
а) 2а2 + 4а – 8; б) а2 (а2 +2а – 4) + 2а ( а2 + 2а – 4).
6. Найдите многочлен М и вычислите его значение при х = -1, если М∙ (х+2) = х3 +2х2 + 2х + 4.
Контрольная работа №5(7 класс). II вариант.
1.Разложите на множители.
а)p2q3 –p3q2; б)x2y2z3–xy3z2+x4y3z5; в) ах–ау+3у–3у;
г) а3+5а2+5а + 25
2. Решите уравнение: а) 5x2+x=0 б)2х3–10х2 +3х–15 = 0
3. Докажите, что выражение а) 96 – 39 кратно 13 б) 1012 +1011 + 1010 кратно 555
4. Разность двух натуральных чисел равна 4, а их произведение равно 96. Найдите сумму этих чисел.
5.Известно, что при некотором значении переменной а значение выражение а2 – 2а + 3 равно 8. Найдите, чему равно при этом же значении а значение выражения:
а) 3а2 – 6а + 9; б) а2(а2 – 2а +3) – 2а(а2 – 2а + 3)
6. Найдите значение многочлена М при х= - 3, если М·(х + 1) = 2х3 + 2х2 + х +1.
Контрольная работа №6. I вариант
1.Преобразуйте выражение в многочлен: а)(а+7)(а – 1)+(а – 3)2; б)(3х – 2у + 1)2; в) (3х – 2а)3; г)(3х – 2у)(9х2 +6ху +4у2).
2.Разложите на множители выражение: а) 121х2 +9у2 – 66ху;
б) (х – 4)2 – 9; в)
х3 – 125а3.
3.Решите уравнение: а)36х2 – 64=0; б)81х – х3 = 0; в)45х2 – 30х+5 = 0 ; г) 5у3 – 4у2 = 5у – 4.
4. Вычислите : 
5. Разложите на множители: а) х3у6 – а3; б)16а4 – 625b4;
в) n2 – у2 +10у – 25; г) а3 – b3 +а2b – ab2
6. Докажите, что число значение выражения 29 + 53 кратно 13
Контрольная работа №6. II вариант
1. Преобразуйте выражение в многочлен: а)(b – 3)(b – 4) – (b +4)2;
б) (х – 5у+2)2 ;в)(3х – а)3 ;г)(х – 5у)(х2 +5ху +25у2).
2.Разложите на множители выражение: а)4х2 +49у2 +28ху; б)
m3 – 64n3; в) 36 – (у – 3)2 .
3.Решите уравнение: а) 9у3 – у5 = 0; б)0,01у2 – 4 = 0;
в) с2 + 4с + 4 = 0 ; г) 2х3 – х2 – 2х +1 = 0.
4. Вычислите : 
5. Разложите на множители: а) 8k3 + a3b3; б)81х4 – 256у4;
в)у2 – х2 – 6х – 9 ; г)а3 +b3 – a2b – ab2.
6. Докажите, что число значение выражения 53 + 212 кратно 7.
Контрольная работа № 7. I вариант.
1.Найдите значение функции: а) у= 2х2 – 5х + 3 при х= - 1; б) у = 
при t = 
2. Найдите координаты точек пересечения графика функции у = -1,7х –51 с осями координат.
3. Найдите область определения функции: а) у = 
б) у = 
.
4. Найдите координаты такой точки графика функции у = 3 – 2х, сумма абсциссы и ординаты которой равна 4. Постройте график этой функции.
5. Задайте формулой линейную функцию, график которой параллелен графику функции у = 5х + 4 и проходит через точку А(2;8) .
6. Найдите корни уравнения: а)х2 = - 3; б) х2 = х+2, используя графики функции.
Контрольная работа № 7. II вариант.
1.Найдите значение функции: а) у = х2 + 3х – 1 при х= – 1;б) у= 
при х= 
.
2. Найдите координаты точек пересечения графика функции у = 1,3х – 39 с осями координат.
3. Найдите область определения функции: а) у = 
; б) у = 
.
4.Найдите координаты такой точки графика функции у = 2 – 3х, сумма абсциссы и ординаты которой равна 4. Постройте график этой функции.
5. Задайте формулой линейную функцию, график которой параллелен графику функции у = 7х – 1 и проходит через точку А(3;24) .
6. Найдите корни уравнения: а)х2 = - 1; б) х2 = 2 – х , используя графики функции.