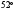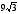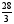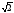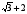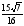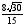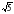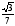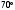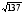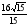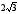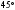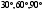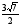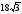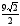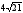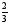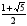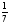Треугольник

ТРЕУГОЛЬНИК

ЧАСТЬ А

1. В треугольнике АВС 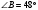, внешний угол при вершине С равен 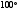. Найдите градусную меру угла А.

2. Площадь правильного треугольника равна 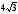. Найдите его периметр.

3. В равностороннем треугольнике радиус вписанной окружности равен 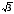. Найдите площадь треугольника.

4. Найдите площадь равнобедренного треугольника с боковой стороной 3 и основанием 4.

5. В треугольнике биссектриса угла, образованного сторонами с длинами 21 и 28, делит противолежащую сторону на отрезки, длина меньшего из которых равна 24. Найдите периметр треугольника.

6. Две стороны треугольника равны 15 и 25, а медиана, проведенная к третьей стороне равна 16. Найдите длину третьей стороны треугольника.

7. Дан треугольник со сторонами 26, 40 и 42. Найдите длину высоты, проведенной к средней стороне треугольника.

8. Найдите сторону МР треугольника MNP, если известно, что .

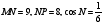9. Стороны треугольника равны 5, 6 и 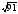. Найдите больший угол треугольника.

10. В равнобедренном треугольнике боковая сторона в 1,5 раза больше радиуса описанной около треугольника окружности. Определите синус угла, образованного основанием и боковой стороной.

11. Найдите сторону ВС треугольника BDC, если известно, что

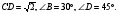
12. Площадь треугольника АВС равна 16. Найти длину стороны АВ, если АС = 5, ВС = 8 и угол

С – тупой.

13. Найдите площадь прямоугольного треугольника с острым углом 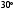и гипотенузой, равной 4.

14. Площадь равнобедренного прямоугольного треугольника равна 36. Найдите длину гипотенузы.

15. Найдите градусную меру острого угла между биссектрисами острых углов прямоугольного треугольника.

16. Катеты прямоугольного треугольника равны 30 и 40. Найдите медиану, проведенную к гипотенузе.

17. Высота прямоугольного треугольника, проведенная к гипотенузе, делит ее на отрезки, длины которых относятся как 1:4. Если высота равна 4, то гипотенуза равна…

ЧАСТЬ В

18. Три высоты треугольника АВС пересекаются в точке О внутри треугольника, причём ОС = АВ. Найдите угол АСВ.

19. В треугольнике АВС из вершины В проведена медиана и высота, которые делят угол АВС на три равные части. Найти углы треугольника АВС.

20. Длины сторон треугольника относятся как 5:12:13. Соединив середины его сторон, получили треугольник площадью 30. Найдите периметр исходного треугольника.

21. В треугольнике АВС величина угла ВАС равна 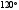, АВ = 3, АС = 5. Найти длину биссектрисы ВК.

22. Дан треугольник АВС, в котором угол АВС равен 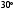, АВ = 4, ВС = 6. Биссектриса угла АВС пересекает сторону АС в точке К. Найти площадь треугольника АВК.

23. В треугольнике АВС проведена биссектриса ВЕ, которую центр О вписанной окружности делит в отношении ВО:ОЕ = 2:1. Стороны АС = 7, ВС = 8. Найти длину стороны АВ.

24. Основание треугольника равно 14, а медианы, проведенные к боковым сторонам, равны 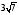и 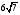. Найти меньшую боковую сторону этого треугольника.

25. Две стороны треугольника равны 6 и 8. Медианы, проведённые к этим сторонам, взаимно перпендикулярны. Найти третью сторону треугольника.

26. Найти площадь треугольника, медианы которого равны 3, 4, 5.

27. В равнобедренном треугольнике боковая сторона равна 20, а основание равно 24. Найти расстояние между точкой пересечения биссектрис и медиан треугольника.

28. В равнобедренном треугольнике АВС со сторонами 40 и 100 проведена высота СН к боковой стороне. Найдите расстояние между центрами окружностей, описанных около треугольников АСН и ВСН.

29. Найдите площадь равнобедренного треугольника, если длина его высоты, проведенной к боковой стороне, равна 12, а длина основания 15.

30. Основание равнобедренного треугольника равно 12, а боковая сторона 18. К боковым сторонам проведены высоты. Найдите длину отрезка, концами которого служат основания высот.

31. В тупоугольном треугольнике основание равно 6, а высоты, опущенные на боковые стороны, равны 2 и 2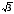. Найдите высоту, опущенную на основание.

32. Параллельно стороне АВ треугольника АВС проведена прямая, пересекающая сторону АС в точке D так, что AD : DC = 3 : 2. Если площадь треугольника АВС равна 50, то площадь получившейся трапеции равна…

33. В равносторонний треугольник вписан квадрат со стороной, равной 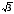. Найдите длину стороны треугольника.

34. Высота треугольника равна 4. Она делит основание на две части, относящиеся как 1:8. Найти длину отрезка прямой, параллельной высоте и делящей треугольник на равновеликие части.

35. Точка М – середина основания АС треугольника АВС. Известно, что АВ = 2, ВС = 3, 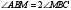. Определить площадь треугольника АВС.

36. В треугольнике АВС АВ = 3, ВС = 5, АС = 6. На стороне АВ взята точка М, на ВС – точка К так, что ВМ = 2АМ, 3ВК = 2КС. Найти длину МК.

37. В треугольнике АВС угол А вдвое больше угла В, а длины сторон, противолежащих этим углам, соответственно равны 6 и 4. Найдите длину третьей стороны треугольника.

38. В равнобедренном треугольнике боковые стороны равны 10, а основание – 12. Найдите радиус описанной около треугольника окружности.

39. В остроугольном треугольнике АВС известны две стороны АС = 8, ВС = 6 и площадь треугольника равн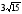а . Найдите радиус окружности , описанной около этого треугольника.

40. Радиус вписанной в треугольник окружности равен 2, а одна из точек касания делит сторону треугольника на отрезки 3 и 4. Найдите площадь треугольника.

41. На медиане ВМ треугольника АВС взята точка К такая, что ВК:КМ = 3:1. В каком отношении прямая АК делит площадь треугольника АВС?

42. В равнобедренном треугольнике АВС сторона АВ=ВС=12. Через середину высоты ВD проведен отрезок МР параллельно стороне ВС. Найдите длину отрезка МР.

43. В треугольнике АВС, площадью 24, точка М лежит на стороне АВ, точка N на стороне BC, точка K на стороне AC, причем AM:MB = 2:1, BN = NC, AK:KC = 1:3. Найдите площадь треугольника MNK.

44. Высота прямоугольного треугольника, проведенная из вершины прямого угла к гипотенузе, равна 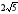. Найдите гипотенузу, если один из катетов равен 6.

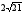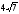45. Катеты прямоугольного треугольника равны и . Найдите высоту, проведенную из вершины прямого угла.

46. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, делит гипотенузу на отрезки длиной 7,2 и 12,8. Найдите площадь треугольника.

47. В прямоугольном треугольнике длина одного катета равна 15, а проекция другого катета на гипотенузу равна 16. Найдите периметр треугольника.

48. Медиана, проведенная к гипотенузе прямоугольного треугольника, делит прямой угол в отношении 1:2 и равна 6. Найдите площадь треугольника.

49. В прямоугольном треугольнике катеты равны 6 и 18. Найдите биссектрису прямого угла.

50. Площадь прямоугольного треугольника равна 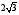. Определить его высоту, проведенную к гипотенузе, если она делит прямой угол в отношении 1:2.

51. Биссектриса острого угла прямоугольного треугольника делит катет на отрезки 10 и 26. Найдите площадь треугольника.

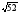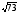52. В прямоугольном треугольнике медианы, проведенные к катетам, равны и . Найдите гипотенузу.

53. В прямоугольном треугольнике АВС с катетами АС = 15 и ВС = 20 проведена высота СН. Найдите расстояние от точки Н до катета АС.

54. В прямоугольном треугольнике АВС из вершины прямого угла В проведена высота ВР. Если выполнено условие АВ = РС, тогда косинус угла А равен…

55. Катет прямоугольного треугольника равен 18. Точка, принадлежащая данному катету, удалена от гипотенузы и другого катета на 5. Найдите периметр треугольника.

56. Два подобных прямоугольных треугольника имеют по катету одинаковой длины, равной 12. Если площади треугольников относятся как 10:9, то площадь большего треугольника равна…

57. Точка на гипотенузе прямоугольного треугольника равноудалена от обоих катетов и делит гипотенузу на отрезки, длины которых равны 30 и 40. Найдите периметр треугольника.

58. В прямоугольный треугольник, катеты которого равны 10 и 15, вписан квадрат, имеющий с ним один общий угол. Найдите периметр квадрата.

59. В прямоугольный треугольник с острым углом 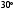вписан ромб так что этот угол у них общий и все вершины ромба лежат на сторонах треугольника. Если длина большего катета равна 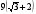, то сторона ромба равна…

60. Периметр прямоугольного треугольника равен 60. Найти его площадь, если высота, опущенная на гипотенузу, равна 12.

61. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 и 12. Найдите сумму катетов треугольника.

62. В прямоугольном треугольнике радиусы вписанной и описанной около него окружностей равны 2 и 5. Найдите площадь треугольника.

63. В прямоугольном треугольнике точка касания вписанной окружности делит катет на отрезки 2 и 6. Найдите расстояние от центра вписанной до центра описанной окружности.

ЧАСТЬ С

64. В треугольнике АВС величины углов А, В, С составляют арифметическую прогрессию. Наименьшая сторона в 4 раза меньше наибольшей. Найти тангенс наименьшего угла.

65. В равнобедренном треугольнике АВС (АВ = АС) с углом 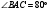выбрана точка М так, что 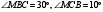. Вычислить .

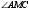66. Боковые стороны АВ и ВС равнобедренного треугольника АВС равны 15, а 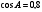. Найдите расстояние от точки пересечения прямых, содержащих высоты треугольника, до точки пересечения его биссектрис.

67. В треугольнике АВС 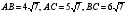. Найдите расстояние от вершины В до точки пересечения высот треугольника АВС.

68. В треугольнике АВС на сторонах взяты точки М, К, N так, что АМ : МВ = 1 : 4, ВК : КС = 2 : 3, АN : NС = 2 : 3. Прямые АК и МN пересекаются в точке Р. Определите во сколько раз РК больше АР.

69. Через точку М внутри треугольника АВС проведены прямые параллельные сторонам треугольника. Площади треугольников, отсекаемых этими прямыми, равны 16, 25 и 49. Найти площадь треугольника АВС.

70. В равнобедренном треугольнике АВС через вершины основания В и С и точку N, которая является серединой высоты, проведённой к основанию, проведены прямые CD и ВЕ (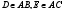). Найти площадь треугольника СЕD, если площадь треугольника АВС равна 27.

71. В треугольнике АВС проведены биссектрисы AD и CF углов BAC и ACB. Найдите отношение площадей треугольников ABC и AFD, если АВ = 21, АС = 28, СВ = 20.

72. Дан треугольник АВС, площадь которого равна 12. На медианах AK, BL, CN взяты соответственно точки P, Q, R так, что АР : РК = 1 : 1, BQ : QL = 1 : 2, CR : RN = 5 : 4. Найти площадь треугольника PQR.

73. В треугольнике АВС медиана АD и биссектриса ВЕ перпендикулярны и пересекаются в точке F. Известно, что площадь треугольника DEF равна 6. Найдите площадь треугольника АВС.

74. В остроугольном треугольнике АВС из вершин А и С опущены высоты АN и СМ на стороны ВС и АВ. Известно, что площадь треугольника АВС равна 18, а площадь треугольника ВNМ равна 2, длина отрезка NМ равна 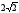. Вычислить радиус окружности, описанной около треугольника АВС.

75. Прямоугольный треугольник, периметр которого равен 10, разбит высотой, опущенной на гипотенузу, на два треугольника. Периметр одного из них равен 6. Найти периметр другого.

76. Точка пересечения медиан прямоугольного треугольника удалена от катетов на расстояния 3 и 4. Найти расстояние от этой точки до гипотенузы.

77. Высота и биссектриса прямоугольного треугольника, опущенные из вершины прямого угла, равны соответственно 3 и 4. Найти площадь треугольника.

78. В прямоугольном треугольнике АВС из вершины А прямого угла к гипотенузе ВС = 12 проведена биссектриса АК = 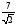. Найдите радиус вписанной окружности в треугольник АВС.

79. В прямоугольном треугольнике АВС из вершины А прямого угла проведена медиана АМ, биссектриса АК и высота АН. Оказалось, что МК = 4 и КН = 3. Найти площадь треугольника АВС.

80. В прямоугольном треугольнике АВС из вершины С прямого угла проведена высота СН. Радиусы окружностей, вписанных в треугольники АСН и ВСН, равны соответственно 5 и 12. Найти радиус окружности, вписанной в треугольник АВС.

81. В треугольнике АВС со сторонами 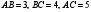проведена биссектриса ВМ. В треугольники АВМ и ВСМ вписаны окружности, которые касаются ВМ в точках К и Р. Найдите длину КР.

ТРЕУГОЛЬНИК

ОТВЕТЫ